Perpetual Motion

Because this is such a lengthy HTML document, I have arranged index marks which the reader can access through the list of contents, below. This is not meant to be a technical discussion. I pulled it together from lecture notes for my sophomore engineering students, sans the mathematics, along with portions of letters I sent in hopes of convincing some science writers that their columns missed the essence of perpetual motion. In this last endeavor I was not successful.

Contents

Introduction

I made an entertaining misstep when I once tried to enlist the help of a machine shop to build a 'perpetual motion' machine. I was head of an engineering transfer program at the time, and I wanted a corridor demonstration that would be intriguing to the public. I thought of a machine that would appear to run without an obvious source of power, but which in fact derived power from a well disguised coil which absorbed energy from the building wiring. I drew up plans and delivered portions to a local machine shop. The owner of the machine shop pointed to a bearing in the plans and asked what type it was.

" Oh, I'll find something," I said, and a couple of days later I returned with a sloppy little bearing that would probably do the job.

" Oh this won't do," the machinist said. " If this is a perpetual motion machine you need a really low friction, precision bearing."

" No," I replied, " this isn't a real perpetual motion machine. This is a fake."

He looked at me oddly, as if wondering why anyone would build a fake perpetual motion machine. I really didn't know how to take his reaction. I thought to explain that there is no such thing as a perpetual motion machine, but decided that I might offend the only machinist who seemed willing to help me. What did it matter anyway? I had an adjunct faculty member who truly believed in cold fusion, after all, and perhaps this machinist truly believed in perpetual motion. On the other hand, he might be thinking I was some sort of cheat trying to perpetrate a fraud. At any rate we continued to miscommunicate for a while longer, and finally let the project die.

The documented search for perpetual motion begins in the 13th century. Villard de Honnescourt drew designs for such machines at that time. There may be earlier designs, but perpetual motion is closely linked to machines, especially rotating machines, and machines are neither widespread nor very sophisticated before this time. Before the invention of electric or gasoline motors there were limited ways to supply power to do work. Waterwheels, tidewheels, and windmills supplied power only in certain locations; man and animals supplied all the portable power. People who had no access to a suitable stream, estuary, or windy hill-top sought alternatives, and inventors attempted to supply them with perpetual motion machines. The search continues to the present day. More recent designs for perpetual motion appear in response to crises, like the energy crisis, or high costs of fuels, or some poorly understood technological need.

What is perpetual motion?

The general public sees perpetual motion inexactly. Probably they view each machine as a special case. The physicist or engineer, on the other hand, is very precise and classifies perpetual motion machines according to which law of thermodynamics they violate. I'll reach this classification scheme presently, but here are some ways to classify perpetual motion machines which are motivated by reading Ord-Hume¹ and Angrist².

1. Magical devices. Our first category is of machines that aren't real, but which get classified as perpetual motion anyway. These operate by no known principle. For example, the self accelerating wheel that has one side shielded with the H.G. Wells material "Cavorite" as in Figure 1.
   

   Figure 1. Our academic grips the guardrail to view the cavorite engine, but losses his mortar board. Notice the large bolts that are required to keep antigravity material attached to the earth.

   
   
2. Impossible machines. Our second category is of machines that defy logic; like the drawings of Maurice Escher, where water runs perpetually down hill, but in a closed cycle. In fact, Escher did make one drawing of a waterwheel run perpetually in such a flow (See Figure 2). Another impossible machine has weights of magnitude "9" on one side which become of weight "6" on the other when the weights turn upside-down.
   

   Figure 2. A small section of an Escher woodcut showing water flowing in an endless circuit. Drawings like these are often called 'ambiguous.'

   
   
3. The next category are real machines, but people often lump them, and perhaps confuse them, with true perpetual motion machines. For instance, a Rube Goldberg machine is simply difficult to analyze and obscure of purpose. Maybe it is intended to work forever, maybe not, but it looks complicated so the typical person thinks it's probably a perpetual motion machine. Into this class also goes any harebrained inventor's scheme.
4. A real machine might be viewed as perpetual motion if it simply runs for a long time. Radioactive decay and rotation of the earth are examples. These actually run down slowly, so they aren't truly perpetual motion machines. They are perpetual only in the sense that they outlast a person's life or memory. (See technical notes.)
5. Foremost among machines intended to deliver perpetual motion are the frauds. These typically are any overly complicated machine running, ostensibly forever, in a completely mysterious cycle of operation with hidden workings (and hidden source of energy). Hiding portions of the workings ostensibly avoids disclosing "proprietary" knowledge about the machine, but also avoids disclosing the inventor as a fake. Examples are the Keely motor (late 1800s) and the machine of E.P. Willis (1850). Keely once suggested that he was "Keely, greatest humbug of the nineteenth century."
6. A large class of schemes are machines that are perpetually out of balance, so that a push start will make the machine run forever, or perhaps even cause it to accelerate. These machines typically remain only in a design stage. If built they may become machines of type 5 above, especially after the disappointed inventor realizes his need to recover expenses. Villard de Honnescourt drew designs for such machines. Seven centuries later and more than one century beyond an understanding of why such a machine will never work, inventors continue to attempt to make the unbalanced wheel spin.
   
   

   Figure 3. Drawing of a wheel that is eternally out of balance. It is sometimes very difficult to explain the mechanical fault that keeps these machines from running. It is much easier to attack their violations of the first law of thermodynamics.

   
   
   An elderly Minnesota farmer³, made the most recent attempt to build an out-of-balance machine that I know of. He had been working for 20 years on a large iron wheel surrounded by a dozen bicycle wheels, complete with springs to continually move the bicycle wheels toward or away from the main axle.
   As of 1973, his wheel hadn't managed more than 12 revolutions before grinding to a halt. Undeterred, however, our Minnesotan presses on.
   " ...its equipment shortage what's tying me up right right now," he says. "I ordered them inner tubes weeks ago and haven't got them yet. But, I think they could be it."
7. Machines based on a misunderstanding of a measurement. In these machines the inventor calculates perpetual motion, he does not actually observe it. An example is the motor of Garabed Giragossian who confused energy with power. The essense of his machine was putting energy into the machine for a long time at low power, and withdrawing the energy for a short period at high power. He managed to convince himself, along with some majority of Congress, that having more peak output power than peak input power is the same thing as obtaining extra energy. What matters is energy. Using peak power as a proxy for energy managed only to confuse everyone, including the inventor.
   Cold fusion, while not a perpetual motion machine, is another example of misleading measurement. Fleischman and Pons calculated a very small excess of energy after making huge corrections to their data, and concluded that this must be derived from fusion even though more plausible explanations were available.
8. Machines without losses or friction are common designs. One is Fludd's closed cycle water pump which raised water into a reservoir by means of a Achimedean screw, and let water run out of the reservoir over a water wheel that turned the screw to raise the water (Figure 4). In order for this machine to run forever, we have to assume that the grinding of grain represents no loss, nor is there any loss to friction. In 1570 a Jesuit Priest, Johannes Taisnierus, designed a machine based on a loadstone, which would pull an iron marble up an incline where it would fall though a hole, roll down a second incline back to its point of origin to begin the trek up the first incline. This machine I discuss in a later section since it appears again and again in articles on perpetual motion. These machine somehow procure energy to offset losses, but there is no source of energy.
   

   Figure 4. The perpetual watermill of Fludd. This machine violates the first law of thermodynamics. In reality it could only operate until its initial supply of energy, which it obtained from the lacky who filled the upper reservoir, is exhausted.

   
   
9. A more subtle class of machines do not obtain energy from nowhere, nor do they leave out friction. They are impossible nonetheless. These machines withdraw heat from a reservoir, perform work, and change nothing else in the universe. They have a closed cycle of operation that brings all parts back to an original state. Proposals for this sort of machine were common before people understood what we now call the second law of thermodynamics. John Gamgee's ammonia motor is an example.
   Gamgee envisaged a motor to propel ships using ammonia as the working fluid. Liquid ammonia boils at a low temperature--well below the temperature of sea water, for instance. Gamgee proposed a liquid ammonia boiler to absorb heat from sea water near temperatures as low as 0°C. At this temperature its vapor expands 4 times until its pressure drops to equal that of the atmosphere. All the while it moves a piston which can turn a ship's propeller. In Gamgee's thinking the ammonia has now expanded so much, and done so much work, that it is cold, and condenses to liquid to begin the cycle over again.
   What Gamgee, and his backers, didn't realize is that the expanded ammonia is cold, but not cold enough to condense. It must expel some additional heat to a colder reservoir to cool further. But no colder reservoir is available, and no condensation ever occurs. The machine never completes more than half a cycle.
10. Perpetual lamps. Here the machine is actually a process (combustion). Fortunio Liceti (1577-1657) made a lifelong study of these lamps, so many of which were supposedly found in old tombs, vaults and temples. Ord-Hume spends several pages examining ways to explain the observation of perpetual lamps. This is giving too much serious attention to a fantasy. It is likely that no one ever observed any such lamp. They belong to the realm of myth like the unicorns and half-man beasts.
    I have found a graphic of a perpetual lamp at an exotic site on the web. You may go to visit it by clicking on the eternal flame. Please return though.

Perpetual Motion and Thermodynamics

Thermodynamics developed from the analysis of machines and processes. Physicists and mathematicians have made it a rigorous science, but its axioms derived from hundreds of years of experience.

Physicists and engineers view perpetual motion precisely and abstractly. In fact, they view the idea of "machine" so abstractly that machines or processes or signals or even algorithms fit the definition. To them any machine violating one of the laws of thermodynamics is a perpetual motion machine. They classify a perpetual motion machine by which law it violates. So a machine violating the first law of thermodynamics is a perpetual motion machine of the first kind. Machines violating the second law of thermodynamics are perpetual motion machines of the second kind, and so forth.

There are very few ideas in physics important enough to call laws. The four laws of thermodynamics are especially important and useful. At one time I examined patents for an industrial company. The question I had to answer was..."will this process or that machine work? Should we buy this patent?" Most machines or processes are too complex to analyze directly in a short time. However, the laws of thermodynamics apply to their operation and make them much simpler to analyze. The analysis begins by abstracting the machine or process to its inputs, losses, and outputs. Then it is simple to apply the laws of thermodynamics to it; and if the machine violates one of the laws, we can send the patent back to the inventor with a polite thank you.

Perpetual motion machines are ordinarily of the first or second kind. However, there is a zeroth law of thermodynamics and also a third law. I know of no one who has written descriptions of perpetual motion machines of the zeroth and third kinds. What would these be like?

Machines of the first kind

The first law of thermodynamics deals with energy, work, and heat. Machines, too, deal with energy, work, and heat. A machine has a supply of energy. As the machine operates it does only one of two things with that supply of energy. It either does work or it produces waste heat. The sum total of the original energy, the work done, and the waste heat have to equal a constant. This is what we mean by saying energy is conserved. How do physicists know that energy is conserved?

They don't know it absolutely, but 300 years of experiment with and observation of machines have never produced a single, credible counterexample.

Perpetual motion machines of the first kind violate this idea of energy conservation. The most obvious machine like this is the perpetual lamp. It produces heat or light, but never drains an energy reservoir to do so. It procures energy from nothingness. Another simple example is the unbalanced wheel, especially the unbalanced wheel with a brake to keep it from accelerating. If a tiny push of the wheel were to set it accelerating, then the wheel would have more energy in its rotation than was put into it with work from the push. Once again, it procures energy from nowhere.

Wheels out of balance are especially interesting machines of the first kind because designs for them occur so often. We can look at them from two different points of view. First, suppose that gravity is what makes these machines operate. Our experience with gravity is that we have to have some amount of mass fall some distance toward earth in order to obtain energy from it. Waterwheels, siphons, and turbines operate according to this principle since in each of these water falls some distance toward the earth. The siphon, in particular, fails to operate if its outlet end is higher than its inlet.

An out of balance wheel, on the other hand, operates without any of its parts falling continually toward earth. Thus, it cannot draw energy from the gravitational field. Likewise, the perpetual watermill of Fludd has no water that continually falls. It procures energy from nowhere and is perpetual motion of the first kind.

Another example is the unbalanced wheel of our Minnesota farmer inventor. He might describe his out of balance machine from a different perspective. The purpose of building something out of balance is to produce a torque once the machine is set in motion. This torque comes somehow from the way the machine parts change position when the wheel is rotating. The torque times the rotation rate supply power to offset losses from friction.

It almost always occurs to the skeptic to debunk out-of-balance machines by explaining why there is no torque to accelerate them. It is not easy to show the mechanical deficiency directly, but it may be the only way to convince true believers of perpetual motion, because they will not accept that any of the laws of thermodynamics apply to their machines. On the other hand it is easy to show that these machines have no source of energy other than the work done to spin them initially. The first law demands that they never accelerate, and the reality of friction means they cannot even spin uniformly forever. They simply drain energy from their initial state. Fludd's waterwheel attains its initial energy from some lacky who drew water to the upper reservoir. The out-of-balance wheel attains it from the initial push.

Machines of the second kind

The first law demands that all machines have a source of energy, but, it doesn't limit how much of this energy a machine can use for work. Could it all be used for work? Could a machine have 100% efficiency?

Even before they knew there was a first law, engineers observed that machines perform less work than the amount of energy they consume. In particular, heat engines always reject some waste heat. For example, an automobile engine always heats the surrounding air, heats water in its radiator, expels heat through its tail pipe, and so forth. The second law guarantees that no clever design could eliminate these losses completely.

The prototype machine of the second kind is Gamgee's ammonia motor. It propels a ship that simply withdraws heat energy from the ocean to power itself. Obviously this doesn't violate the first law, because the ocean contains plenty of heat energy. The ship would simply extract some of it, leaving a cold wake behind. Losses from friction in the ship's propellers and shafts would would return some of this energy to the ocean immediately. Stopping the ship at its destination port would turn the remainder to heat and return it to the ocean as well. The ship would merely borrow energy for its voyage from the ocean. Experience shows that such a machine can't be built.

Perpetual motion machines of the second kind operate by extracting energy at some point in their cycle, use it for work, yet have everything return to an original state unchanged at the end of the cycle. There is the appearance of being able to deliver energy forever. Real machines and processes leave the universe changed permanently. Engineers measure this change as entropy; and the second law demands that any real process increase the entropy of the universe. Two familiar examples will show what this means.

It is possible to decrease entropy over a portion of a machine cycle or in a part of a machine, but the remaining cycle produces more than enough entropy to make up for it. For example, it is possible to decrease entropy by cooling the innards of a refrigerator, but only by producing much more entropy in the wiring, motor, and compressor that run the refrigerator.

Everyone is familiar with the flow of heat. If we place objects of different temperature together, we always observe that the objects all come to the same temperature. It never happens that among objects all at one temperature, some will spontaneously become hot while others become cold. In the first situation the entropy of the universe increases, as expected; while in the second situation it decreases. The second situation can happen only if heat could flow spontaneously from cold objects to hot ones. Thus, the second law implies that heat always flows spontaneously from hot to cold. This makes temperature difference a type of force that causes heat flow. Obviously, it is possible to make heat flow from a cold place, like the interior of a refrigerator, to the warmer kitchen; but, this happens only if we put work into the cycle through the electrical motor.

What this has to do with engines is not obvious, but I'll try to explain it now. To make a heat engine work we must make heat energy flow into it. The only way to do this is to connect it to a reservoir that is hot. Heat energy will flow into the engine, which converts some of this heat to work. However, doing nothing more than absorbing heat would decrease entropy. So the heat engine has to expel waste heat to another reservoir, and, the only way to do this is have a reservoir that is colder than the engine. Also, because the engine used some of the heat energy for work, there is less heat to expel to this cold reservoir than was absorbed from the hot one. Thus, to use rejected heat to offset the decrease of entropy from absorption, the reservoir for waste heat has to be much colder than the hot one. The more temperature difference there is between the two reservoirs, the more work we can perform with the engine and still manage to increase entropy. Large temperature differences result in a large "thermal force" to run a machine efficiently.

Figure 5 shows an extremely simplified analysis of an ideal engine; one that physicists and engineers call a Carnot engine. In the four segments that make its cycle, the engine absorbs heat, does external work, expels heat, and finally absorbs some of its own capacity for work as it returns to its initial state. It represents the most efficient heat engine possible, which is why Rudolph Diesel purposely designed his engine to approximate this cycle. I'll return to this figure when I discuss third law machines.

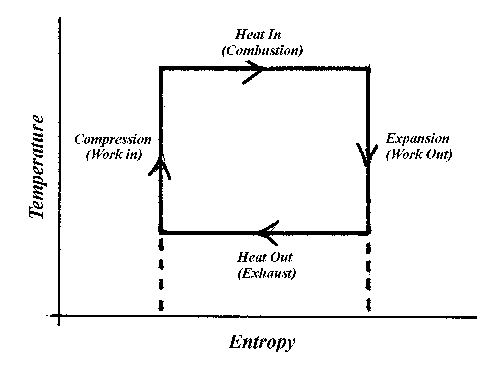
Figure 5. A cycle on a T-S (Temperature-Entropy) diagram to represent a Carnot process. I have added labels to identify 4 distinct segments of the cycle to make it comparable to an engine, like a diesel engine.

Machines of other kinds

As I said earlier, physicists begin counting laws of thermodymanics from zero, and they don't stop until three. Do machines of the zeroth and third kind exist? What sorts of machines are they? I do not know of any discussion of machines other than the first or second kind; so, what now follows is pure speculation.

Machines of the zeroth kind.

The zeroth law of thermodynamics deals with thermal equilibrium. It states that temperature is the measure of thermal equilibrium, and that temperature works as follows. Let "A", "B", and "C" be three different things. If "A" is in thermal equilibrium with "B" ("A" and "B" have the same temperature), and "B" is in thermal equilibrium with "C" ("C" and "B" have the same temperature), then "A" and "C" also have to be in thermal equilibrium ("A" and "C" have the same temperature). This law is so reasonable that we all may wonder why we even need it. Yet, without it we have no justification for using a thermometer. I shall show, now, what it has to do with perpetual motion.

Remember that a difference in temperature means that heat will flow spontaneously between two objects, and the flow of heat also means we can do work. Suppose that "A" and "C" are small reservoirs for storing heat; like water baths, for example. Putting in or withdrawing heat from them will change their temperature. Suppose "B" is a huge reservoir. No amount of heat extracted from it or rejected into it ever changes its temperature.

The zeroth law machine depends on the truth of the following scheme. Reservoirs "A" and "B" have the same temperature, and "B" and "C" have the same temperature, but "A" and "C" don't have the same temperature. Then we can disconnect "A" and "C" from the big reservoir, connect them together through a small engine. The reservoirs "A" and "C" will transfer heat, run the engine, and eventually come to the same temperature. Now reconnect them to "B" to begin the process again. This machine will run forever, and is a machine of the zeroth kind.

Our discussion to this point is abstract, but we can find examples of such machines by noticing their essential feature has heat (energy) running in an endless loop. Impossible machines like Maurice Escher's perpetual watermill (Figure 2), or the flow through flask of R. W. Heinze⁴, are machines of zeroth kind. The impossible class in fact fits perfectly, because the zeroth law states something both physically and logically reasonable; so to deny it ought to lead directly to impossibilities.

Something else that I had noticed about zeroth-law machines, but which I didn't see as important until I recently found something written about zeroth law machines¹¹ is how similar they are to second law machines. For example, if we cover up all of the details concerning my hypothetical zeroth law machine except the work output of the heat engine, then the zeroth law machine looks exactly like a machine that withdraws heat from a reservoir, performs work, and does nothing else. In other words, it looks like a second law machine. If it is possible to build a zeroth law machine, then it is possible to build a second law machine.

Machines of the third kind

People state the third law in several ways. Nernst stated it as "...entropy change of a process acting between equilibrium states tends to zero at absolute zero..." Because I haven't explained anything about entropy or equilibrium, and I don't intend to do so, the third law is easier to understand if I state it as "...no process can reach absolute zero in a finite number of steps..."

The third law has lead a checkered life, as Zemansky⁵ puts it, replete with controversy and confusion. It took some thirty years from the time Nernst first annunciated it for most physicists to finally agree on its wording and meaning. Some, like Rolf Haase, maintain that in some cases the 3rd law results directly from the 1st and 2nd laws, sometimes the 3rd law is more complicated than the Nernst theorem, and, in any case, the 3rd law isn't worthy of being called a law. On the other hand, C.B.P. Finn states that consequences of the 3rd law are observed experimentally, and this is evidence of its validity and importance.

So far I have left mathematics out of my discussion, but to illustrate perpetual motion of the third kind I need just a little mathematics. The second law states that exchange of heat leads to a change of entropy. Mathematically, entropy change dS when a small amount of heat (dQ) enters a reservoir at temperature T is dS = dQ/T. What matters at this point is that a rearrangement of our equation to dQ = T•dS demonstrates that knowing the entropy change and temperature along a curve in the T-S plane is equivalent to knowing how much heat got transferred when the machine or process evolved along the curve. Since heat and energy have the same units, integrating T•dS also represents an exchange of energy. By means of a graph that plots T against S a person may analyze the operation of a machine or process. Note also that in rearrangement of the second law I glossed over the problem of what happens when T is zero; this problem becomes apparent in a moment.

The graph of T against S shown in Figure 5 physicists call a Carnot cycle. It represents an ideal machine that runs by withdrawing some heat from a high temperature reservoir and rejecting waste heat to the low temperature reservoir. The rejected heat is unavailable for work in the present cycle; so, the machine has an efficiency less than 1.0. None of the details of the machine have any importance at the present time, except to note that the Carnot engine is the most efficient heat engine possible that works between the two reservoirs.

The amount of work the Carnot engine does equals the area enclosed by the cycle. Because the Carnot cycle operates over a rectangular cycle in the T-S plane, the calculation is trivial. Work equals the change in S times (T_h-T_c) while the heat withdrawn is just the change in S times T_h. So efficiency becomes 1-T_c/T_h. An efficiency of 1 is possible if T_c equals absolute zero. Being able to expel waste heat to a reservoir at absolute zero makes it possible to build a machine with efficiency of 1 without violating the second law; or in other words, to build a machine that withdraws heat from a reservoir, does work, and has no other effect on the universe. The 2nd Law is satisfied since an infinitesimal amount of heat rejected to a reservoir at T_c=0 could increase entropy enough to offset the decrease that occured in drawing heat from the high temperature reservoir. This is where dividing by zero in the definition of entropy comes back to bite us. Not having a third law leaves the door to the perpetual motion work shop ajar. A perpetual motion machine of the third kind is one that has a cold reservoir at absolute zero.

However, to make practical use of such a cold reservoir, a machine has to reach absolute zero in a finite number of steps. This means that the two curves of constant entropy in Figure 5 (called isentropes) have to reach absolute zero without intersecting, just as the dashed curves in Figure 5 portray. The Nernst statement denies this possibility. The third law closes this last loophole in thermodynamics.

In the discussion of first law machines I stated that such machines work only until they exhaust their initial supply of energy. For example, the out-of-balance wheel will turn until friction exhausts its initial supply of kinetic energy. However, what if we can make a machine that has no friction? If we provide it with a push, then it can spin without violating any law of thermodynamics, and without friction it will spin forever. Therefore we have a perpetual motion machine, provided that we not try to extract useful work from it. Fortunately no one has ever been able to escape dissipation of some sort--friction, viscosity, electrical resistance-- in any machine or process operating on principles of classical physics. This dissipation means, in effect, that a machine rejects heat to some reservoir--a bearing, resistor, lubricant--above absolute zero. Proposing frictionless machines constitutes proposing machines of the third kind.

Finally, I have an example of a third law machine related to a widely believed science-fiction. This is the idea that our television signals have dribbled out into space, and that some advanced race on a planet 30 light years away has received these accidental signals, and might retransmit them back to us. The transmission path from earth to distant star is a communications channel and when the rate of transmission of information exceeds the channel capacity, errors soon dominate the transmission. As a signal spreads far into space its energy density diminishes. It remains detectable only so long as it is resolved against the background sky, or until thermal noise in the receiver buries it. Of course, this point depends upon many things, but let's take a reasonable example. Suppose the TV transmitter can broadcast one-millions watts in all directions. Assume that the information content in an old black and white TV transmission requires 5 MHz bandwidth, just what the FCC makes available. Finally presume that our space people have a one kilometer diameter dish antenna connected to a receiver with a noise figure of 3K. Then the information rate of the broadcast signal exceeds the capacity of the communications channel at the orbit of Pluto. Beyond Pluto the broadcast is buried in snow. In order to decipher the TV program at still greater distances requires a background temperature and receiver noise figure that are below the cosmic microwave background. Proposing that space people can watch old broadcasts of I Love Lucy at any distance if they simply wait long enough, is proposing that space and the receiver have an effective temperature of 0K; that it is a machine of the third kind.

Current state of perpetual motion technology

Ord-Hume claims that interest in perpetual motion is dying. He thinks this is so because modern life provides so many distractions that we have neither time nor inclination to think about perpetual motion. Perhaps, too, interest has waned with the passing of the tinkerer. Apparently, Ord-Hume hasn't looked very hard for tinkerers. They are all over the internet. As for interest in perpetual motion, he hasn't attended any free energy or cold fusion fairs either. There is still enormous interest in subjects akin to perpetual motion. An advertisement run in 1967 brought 41 inventors of perpetual motion machines out of the bush⁶. Interestingly, most of the proferred designs were of wheels out of balance. High Energy Research and Lindsay Publications both have for sale perpetual motion videos, papers, and books. The world of scam energy devices is thriving.

Even if it were true that general interest in perpetual motion is waning, it still provides an eternal topic for writers of science columns. Sometimes, though, the descriptions and analyses are more baffling than perpetual motion itself. What seems true is that analysis of perpetual motion follows paths established long ago, and sometimes misses the point of why some scheme won't work. A few examples dredged from the popular science press illustrate this.

A writer for Radio Electronics Magazine, for example, complained in 1992 that he receives several requests per week for perpetual motion information⁷.

"Looking for free energy systems is dumb," he says.

I agree, because I know it is impossible. However, the science writer thinks it dumb because

"...it will hasten the ongoing entropic death of the planet."

He implies that perpetual motion of the first kind, the free energy variety, is possible, but environmentally undesirable. This is appalling reasoning from someone who is otherwise technically astute.

Two machines featured in an OMNI column several years ago further illustrate my point⁸. One isn't even a perpetual motion machine, while the other illicits confusion over why it won't work. My protests to the author of the column earned me a let-me-repeat-myself-because-you-obviously-don't-understand rebuke.

The Schadewald gravity machine

Bob Schadewald, a science writer, supposedly proposed this contraption as an April Fools prank. However the analysis of the OMNI editor⁸, doesn't accurately portray it.

Schadewald's machine is a lopsided wheel started with its heavy end at the top. It's obvious that someone had to put some energy into this wheel to get it into this position. So the wheel begins with some energy. Now if the wheel is allowed to rotate, this potential energy is converted into kinetic energy (rotation). In fact, we can state this precisely. The wheel picks up speed until its lopsidedness is closest the ground, then it slows down until it returns to the original position. If H is the maximum difference in height of the center of gravity of the machine as it turns, then mgH is the maximum amount of kinetic energy at the bottom of each turn, which is converted back into potential energy as rotation lifts the heavy side of wheel again. This is merely the cyclic conversion of mechanical energy between two forms.

But Schadewald adds a confusing element, he supposes that the universal gravitation constant G, diminishes with time. What does this do?

According to Schadewald, with tongue in cheek I presume, and some later authors, it makes his wheel a perpetual motion machine because it is constantly gaining energy. He reasons that if g₁ is the acceleration of gravity at the end of one cycle of rotation, and g₂ is the value at the end of the next cycle, then G declining during each rotation leaves mg₁H>mg₂H. The machine allegedly gains rotation energy with each turn. This is a spurious argument in that it avoids accounting for all the energy. I said earlier that mgH is the maximum kinetic energy at the bottom of each cycle. According to Schadewald, it is also the maximum energy gain of the wheel. If we add rotational energy to potential energy at any position in the rotation, we find the two add to a constant.

We don't have to propose something as exotic as having G decline to build this machine. We could place Shadewald's machine in the cargo bay of the Space Shuttle and turn it loose when the vehicle passes through maximum "G-force" during a launch. As the shuttle reaches orbit the Shadewald machine would behave just as it would if G were to decline to zero. Of course, friction eventually brings the Schadewald engine to a halt, but this is beside the point. Schadewald's gravity engine is no more than a flywheel, given a spin, and expected to turn forever in the absence of friction. With each turn some spin is carried forward into the next revolution. Eventually our lopsided wheel turns smoothly (even if the bearings notice a cyclic force). But this rotational energy didn't appear spontaneously, and it has nothing to do with diminishing G. Potential energy was originally assembled into the machine back when G was G, and this is now the energy of rotation. Dropping the value of G slowly allows the wheel to turn, eventually, at a constant rate; but beyond this it does nothing. There are no violations of thermodynamics. There is no perpetual motion machine to speak of here at all.

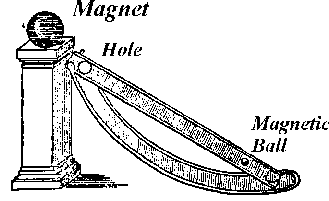
Figure 6. Taisnierus Lodestone Motor. This is a staple of discussion on perpetual motion. Unfortunately people get bogged down explaining the mechanical deficiencies of the device rather than explain why it violates the second law of thermodynamics.

The Taisnierus Magnetic Engine

The second machine often explained badly is that of Johannes Taisnierus which I show in Figure 6, above. A permanent magnet (lodestone) pulls an iron ball up an incline. But the incline has a hole in it which the ball, stupidly, falls though. This returns the ball down a slide through a lower hole onto the incline, where it resumes its climb back toward the magnet. The endless cycling of the ball is supposedly perpetual motion.

In analyzing why this machine will not work, the OMNI editor repeats the same flawed analysis that Angrist² used (see the first of my notes, though, for a revision of this). He says,

"...any magnet strong enough to pull the ball up a ramp will pull the ball over the hole. That seems obvious⁸..."

That is not obvious and it misses the entire point of why the machine is impossible. What this suggests is that the machine won't run because it has a flaw in its mechanical design. Is this a perpetual motion machine, or is it simply a bad design? This explanation evades analysis of the machine as a thermodynamic impossibility.

It is quite possible to construct the incline so that the force of magnetism up the plane exceeds the force of gravity directed down the plane. The ball will roll up the plane. It is equally possible to have the magnetic force at the location of the hole directed upward be less than the force of gravity straight down the tube. The ball will then fall down the hole. The tube has less incline than the plane at some point because it delivers the ball back onto the plane, so the ball will accelerate down the tube at first, then decelerate, then roll out on the inclined plane, then roll up the plane again as long as it can avoid the lower hole. Thus, as long as we neglect friction and losses, it is possible to design the machine for perpetual cycling. In fact, the fake perpetual motion machine that I alluded to in the introductory section ostensibly works on the same principle. There were designs in the Amateur Scientist Column, many years ago, for magnetic machines very similar to Taisnierus' design that behaved like perpetual motion machines except they had a hidden source of energy.

Why, then, will the machine as Taisnierus designed it not work? The reason is that the ball will lose a small amount of energy to friction during each cycle. So the ball will come to a halt at a different place on the ramp than where it started. To place the ball exactly back at its starting point requires that something add a little energy to move the ball to the right point. Otherwise the ball eventually comes to rest somewhere on the lower ramp. The tiny amount of energy added each cycle keeps the real machine from becoming a perpetual motion machine.

Some Unusual Topics

The garbage chimney

A professor I knew at University of Utah had lots of creative suggestions for projects. He was also a terrible kidder, and could say the most outrageous things with a straight face.

He once proposed that we build a chimney of some light material, like Kevlar, up though the atmosphere, and evacuate the chimney with a vacuum pump. At its lower end we put an air-lock. We put garbage into the air lock, open the vacuum side, and blow the garbage far into space. He swore that once evacuated, the chimney would work perpetually. The entire contents of the airlock blow clear leaving the lock ready for the next load of disposable diapers. I laughed, thinking it all a joke. He didn't even smile. Was he serious, or pulling my leg? I dunno; but, whatever his intent, his scheme provides an example of using thermodynamics to examine a process.

A machine like this is pretty complicated to analyze thoroughly. Open the airlock, and garbage and air go all over the place. Exactly where everything ends up is not easy to say. Despite this complexity it is easy to show that this machine won't work as advertised. If it does, it becomes a perpetual motion machine of the first kind. You see, we can boost garbage into space, where it has lots of both potential energy, by virtue of its height above ground, and kinetic energy, by virtue of its having reached an orbital speed. Supposedly we can do this without end. However, this energy has to come from somewhere, but the only initial work that we did was to pump air out of the chimney. Thus, we propose to do an arbitrary amount of work from a limited initial supply of energy. The scheme is just like a perpetual watermill. It is a machine of the first kind.

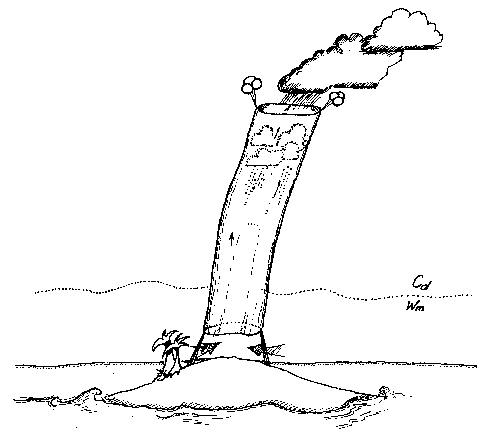
Figure 7. José Peixoto's proposed rainmaker on a desert island. The two layers of air are dry air, that may also be cool, C_d overlying a thin layer of warm moist air W_m. Once we fill the tube with buoyant air the machine can run on its own, drawing energy from the density difference between moist and dry air.

A Perpetual Rainmaker

In the 1960s José Peixoto, a famous climatologist, proposed that engineers in the Middle East take control of the hydrological cycle, and build a perpetual rainmaker. Figure 7 shows his scheme. A tube of some light material, like Kevlar, is erected straight up to a height of 3000m or so. Moist air is always plentiful in a thin layer near coasts in the Middle East. If we initially force some of this air up the chimney somehow, it will cool as it rises, and rain out its moisture. Soon we have warm, moist air flowing in at the bottom; cool, dry air flowing out the top; and a perpetual shower of fresh water to gather on the ground.

Surely this sounds like a perpetual motion machine. Is it one?

The rainmaker is not a machine of the first kind. A machine of the first kind produces unlimited work from a modest initial supply of energy. In the rainmaker, we provide the modest initial energy by forcing warm moist air up the chimney. However, once it is running on its own, the rainmaker taps into an energy supply of its own. This is the latent heat of water vapor in the moist air.

Is it a machine of the second kind? Once again the answer is no; because it absorbs heat from a high temperature reservoir, the moist air, and rejects some to the cool air outflow. In fact, we can draw a T-S diagram for its operation by knowing what the air is like at the intake and outflow. I hesitate to launch into a discussion of how to do this, but Figure 8 shows an approximate diagram for the rainmaker. The section of the cycle labeled with a circled "1" is the portion of the cycle that is apparent in the machine itself. Here moist air rises on what the meteorologists call a "pseudoadiabat." The other three portions of the cycle occur outside the rainmaker. Section 2 occurs as the cool, dry air expelled from the top of the chimney mixes with its environment and radiates heat to space. Section 3 occurs as this mixed air descends toward the ocean surface again, and section 4 occurs as the air picks up heat and moisture from the ocean surface on its way back into the rainmaker.

From this description, and the diagram, rainmaker behaves much like a house-broken hurricane, and has about the same efficiency.

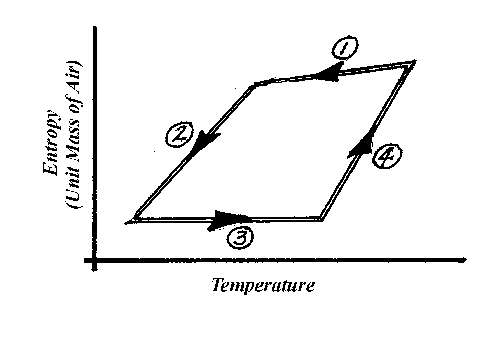
Figure 8. Temperature-Entropy diagram of the rainmaker. I describe in the text the four separate sections of its cycle.

Plate tectonics

The question "What is the driving force of plate tectonics?" has occupied the minds of geophysicists for 40 years. There are several possible sources of energy, but a majority of geophysicists would likely agree that heat flowing from the mantle to the surface is a likely candidate. Figure 9 is a cartoon of how this works. Hot material rises from the deep mantle to the base of the lithosphere in the upper mantle at a spreading ridge. Here it flows laterally rejecting heat all along the way. This heat gets conducted to the earth's surface. As it cools, the lithosphere thickens. Eventually the lithosphere is forced, somehow, back into the mantle where it must melt, mix back into the bulk material, and reappear millions of years later at a ridge again. As the material descends and mixes, it absorbs heat.

The plate tectonic cycle is, therefore, a heat engine. The amount of heat it rejects amounts to 0.04 watts/m² averaged over the entire earth, which seems quite insignificant when one considers that this is enough energy for only one reading lamp every 100m². Solar energy is ten-thousand times larger.

The situation is even worse because the second law of thermodynamics says that not all of this energy is useful for work. Lower and upper mantle have little temperature difference between them. Perhaps the temperature ranges from 1500K to 1300K. The tectonic engine probably has much less efficiency than a Carnot engine, but even a Carnot engine running between these temperature limits has only 15% efficiency. Thus, as a heat engine plate tectonics suffers from having little energy density, compounded further by poor thermal efficiency. No wonder the plates move so slowly.

What other possibilities exist? Perhaps the low temperature at which heat is rejected is less than 1300K. Perhaps some heat being conducted through the lithosphere, especially near spreading ridges, aids the tectonic engine through thermal expansion. Even if the effective temperature of the cold reservoir were 1000K, the engine could be no more than 30% efficient. It's still an underpowered motor.

A number of geophysicists propose that density differences between various materials shown in Figure 9 run the tectonic engine. Refer to the cartoon again. Near the spreading ridge, material in the upper mantle changes composition as it melts (it fractionates). I've denoted this area with cross-hatch in the figure. This low density material rises and crystallizes to form the ocean crust. As the lithosphere ages, cools, and thickens, its lowermost part undergoes a phase change to a dense form of material. I've shown this as cross-hatch in the subducted slab. This dense material sinks back into the mantle, and pushes the circulation of material¹⁰.

At first glance this proposal seems to supply an enormous amount of potential energy for the tectonic engine. However, if it continues to run in this cycle, plate tectonics is a perpetual motion machine, because the working fluid passes around a cycle, ending where it began in unchanged form without having changed anything else in the universe except to expel some heat. Heat-flow, once again, is the only irreversible change that this model exhibits, which limits its efficiency to that of the Carnot engine.

There are other possibilities. Perhaps there is a permanent chemical change in addition to heat flow. That is, less dense material is incorporated continually into the crust while more dense material slowly settles to the lower mantle or core. This would act to stir the mantle. Then again, there might be other mechanical sources of energy. Tidal drag, for example, might convert some of the Earth's rotation into ciculating material in the mantle.

Whatever the ultimate answer, analyzing plate tectonics as a machine with the aid of thermodynamics will probably produce some surprising results.

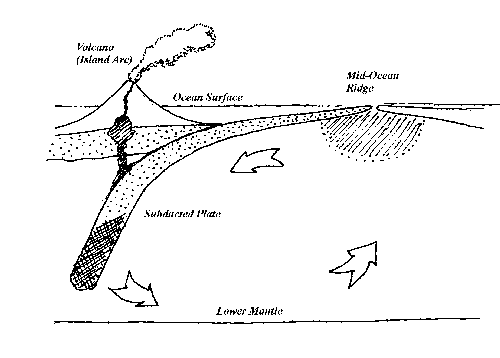
Figure 9. Cartoon of the plate tectonic engine that runs oceanic spreading, subduction at plate margins, and island arc volcanism. The cross hatching indicates places where there is a phase change and an accompanying change in density.

How hot can we focus the sun's rays?

One last example is unusual because it involves a problem that doesn't seem related to machines or work. Little boys, we know, like to burn things with magnifying lenses by focusing the sun on them. Can this focus be made hotter than the sun itself?

Suppose for a moment that the focus is hotter than the sun. Then it is possible to build the following contraption. Focus sunlight on some kind of input to a heat engine. Because we assume this focus is hotter than the sun itself, heat will flow back to the sun spontaneously. So, we can arrange the heat flow through the engine to do some work and expel waste heat back to the sun. In other words, the sun is a source of heat energy, and also is the dump for waste heat. This is the Gamgee Ammonia Motor all over again done at very high temperature. It is a machine of the second kind. Our assumption that the focus could become so hot is obviously wrong.

Bibliography

• 1. Arthur W.G.H. Ord-Hume. 1977. Perpetual Motion: history of an obsession. St. Martin's press. New York. (Keely quote p. 147)
• 2. S.W.Angrist. 1968. Perpetual Motion Machines. Sci. Am. 218:114-122, January.
• 3. Newsweek. Man in motion. 82:84, N 5 73.
• 4. R.W. Heinze. 1948. Why perpetual motion won't work. Sci. Digest. 24:42-46. August.
• 5. Zemansky, M. Temperatures very low and very high. Dover. 1964.
• 6. M. Lamm. 1967. Hooray for the human spirit, human spirit, human spirit... Esquire 68:142-143, Dec. Lamm notes that perpetual motion machine inventors never collaborate so they are doomed to design the same things over and over.
• 7. D. Lancaster. Perpetual Motion Again. Radio. Elec. 63:77-79, Feb 1992.
• 8. S. Morris. 1990. Perpetual Motion-- why will these machines stop? OMNI 12:98-99, july.
• 9. C. B. Hicks. 1961. Why won't they work? Am. Heritage. 12:78-83 April.
• 10.R. A. Kerr. 1995. Earth's Surface May Move Itself. Science. 269, 1214-1215.
• 11.R.K. Wangsness. 1971. Perpetual motion of the zeroth kind. AJP 39, 898-900.