How to freeze to death in Wyoming in the summertime

and other paradoxes of radiation

A seminar presented March 14, 2001
at LCCC Star Club, Cheyenne, Wyoming
by
Dr. Kevin T. Kilty

Those of you who have taken a two semester course in general physics or even a two semester course in engineering physics may have gotten some introduction to the topic of this seminar. You know that all objects warmer than absolute zero radiate electromagnetic radiation. You were probably introduced to the Stefan-Boltzman law, which relates the total power radiated from a hot object, per unit area of surface, and into a 2p steradian solid angle, to the temperature of the object. For those of you not familiar with solid angles, a solid angle of 2p is a hemisphere. In other words, this represents the entire view above a plane surface; or, if you wish, this is the biggest view in which none of the plane can "see" any portion of itself. Stefan's Law is

Power=seT⁴; where T is the absolute temperature of the body and two leading constants represent, respectively, the Stefan constant and the emissivity of the body; e=1 applies to a special type of surface known as a blackbody.

In some instances you may have seen Stefan's Law modified a little bit to account for radiation coming toward the object from its surroundings. Letting T_o stand for the "effective" black body temperature of the surroundings, the modified law is

Power=se(T⁴-T_o⁴)

This at least acknowledges the importance of the surroundings, but is otherwise pretty worthless because we have no means for calculating T_o!

Perhaps you also learned of Wein's displacement law, which states that the peak wavelength of this broadband thermal emission is proportional to 1/T. In fact, if we measure wavelength in units of micrometers, then a good approximation is l=3000/T. Thus, the sun at 6000K has a peak wavelength just about where our eyes detect green light at 0.5m, a human being at 300K radiates with peak power near 10m, and the cosmic background at 3K has a peak in its spectrum near 1mm.

More than likely this is all you learned. What you didn't learn is that what you did learn is completely inadequate to work the simplest of heat transfer problems involving radiation.

What an engineer would like to know.

Engineers have to solve practical problems. Their solutions are tested when a design is first put to use. This means that they can't solve the sort of wimpy problem we typically find in a physics textbook--something like "what is the heat radiated from a one-liter teapot filled with boiling water?" But armed only with Stefan's Law, this sort of problem is the extent of what a person can solve. Engineers need to find answers to the following types of questions:

• How much heat will an object transfer through radiation to some other object?
• What will be the equilibrium temperatures of a collection of objects in a field of radiation?
• How will the temperature of some object evolve?
• What will happen if I alter a design?

How do we go about answering such questions?

In order to answer any such questions we have to modify and extend the Stefan Law because it deals only with the emissive power of a hot object. We can do this as follows.

• First, we ask, "How will objects absorb and reflect radiation?" From the first law of thermodynamics, or conservation of energy, if you will, it is apparent that the total of reflected, absorbed, and transmitted energy must be constant. There is no other place for energy to go. Therefore, using r, a, and t as the coefficients involved, the first law is r + a + t = 1. From the second law of thermodynamics it is true that a = e, this is known as Kirchoff's Law. You can verify this by noting that you cannot distinguish objects, no matter how different they may be from one another, if they are isothermal--inside of something like a kiln, for example.
  Strictly speaking all of these coefficients vary with wavelength, so Kirchoff's Law should actually read...
  
  a_l = e_l
  
  
• Next, to account for the disposition of all energy transferred among or between objects we need to define...
  • J=Radiosity which is the total radiant power leaving the surface of an object. Not all of this has the object emitted. Some is reflected from other objects or transmitted from behind.
  • G=irradiation which is the total radiant energy falling on a surface.
  • W=emissive Power which is the total power emitted by the object by way of its absolute temperature.
  
  
  Of course, it goes without saying that all of these quantities are per unit area of surface and per hemispherical solid angle.

  An example relationship among these is J=W+rG, which holds for objects that are not transparent to radiation. I have an example showing the distinction between radiosity and emissive power.

• Third, because all quantities are stated per unit surface area and per solid angle of the view, then heat transfer depends on both surface area and orientation of surfaces with respect to one another. In other words, there are ugly four-dimensional integrals lurking about.

  For instance, figure 1 shows a series of surfaces where (1) is a radiator and (2) is an absorber. Despite the surface areas involved being the same in each case, the heat transfered q_1->2 is different for each because the view of one another is different. Engineers generally hate to do four-dimensional integrals, so the more mathematically inclined among them will always compile tables of factors for various shapes and orientations. Most engineering texts on heat transfer contain such tables.

  
• Finally, to account for behavior of materials which are not ideally black, we allow that e_l<1 and that it varies according to material. The actual values have to be found from experiments.

For a blackbody we can use these methods to modify Stefan's equation to pertain to two surfaces which are exchanging radiation. Let q_1->2 be the total heat transfered from (1) to (2) per unit time. Let F_1->2 be a heat transfer factor, which engineers call a shape factor. This is that four-dimensional integral we can read from a table. Let T₁ and T₂ be the absolute temperatures of the two surfaces. Then

q_1->2=A₁F_1->2s(T₁⁴ - T₂⁴)

This equation is far more useful than even the modified form of Stefan's Law because it tells us the heat transferred between two specific surfaces at specific temperatures. In other words, between two objects in a design.

If the objects in question are not black, but grey, then rather than use absolute temperature we use radiosity. The radiant exchange from surface (s) to (t) is

q_s->t=A_sF_s->t(J_s- J_t)

If there are more surfaces involved than two, then the above equation simply contains more terms on its right hand side, and there are equations for each object. In this case the solution involves a system of equations.

Note the following very useful fact. If we think of q as a "current," J as a "voltage," and 1/(AF) as a "resistance," then the problem of finding the equilibrium heat transfer rates among a collection of objects is just like a DC electrical network problem. If we seek equilibrium radiosities (or temperatures), instead, the problem is an inverse DC electrical network problem. In other words, any sophomore engineering student who had taken my intro to engineering 1610 course, could work such problems. In particular, they could explain the paradoxes which follow.

Some paradoxes involving radiation.

The firetruck fiasco.

In the autumn of 1979 a condominium building, which was under construction, caught fire in north Cheyenne. When the firemen arrived at the scene, there was one end of the building which was not on fire, and they proceeded to pull their firetruck -- a nice, new, very expensive firetruck -- alongside of this wall.

I do not know why what happened next did happen. I'm sure there was some inquest at a later time, but I do not know its findings. What happened was that the entire building, including the wall adjacent the firetruck, being a tinderbox, was soon an inferno. This is entirely expected in an open wooden structure. What I do not know is why the firemen failed to notice that the entire building was about to be engulfed in flames, and why they failed to take their truck a safe distance away. Perhaps, and this is entirely understandable, they reasoned as follows. Their experience is that it is safe to stand twenty feet from a roaring fireplace, and since this inferno is no hotter than such a roaring fireplace, then twenty feet is a safe distance for our truck. With nothing more than Stefan's law as guidance one could easily misapprehend the implication of solid angle in the formula. In brief, a roaring fire at twenty feet subtends a very small solid angle; a blazing building at twenty feet is something different altogether.

We now appreciate the predicament of the firemen. Their pumper was nearly out of water, and the driver's side of the truck was searing in radiation equal to 30 or maybe 60 summertime midday suns. It got hot very fast. The plastic melted. The paint bubbled and peeled. The tires caught fire and exploded. The truck sat next to the burnt out ruin of the condos for a week or more as a sort of monument to misunderstanding solid angle.

What's the heat-flow deal if we are inside? Why do heated rooms feel cold?

Everyone knows that there is something "funny" about building temperature control. A thermostat in any building is placed, by statute, where it can't measure the effective temperature of the room. Figure 3 shows a room with a very large window, providing a wonderful view. The outside air temperature is 0°C (273K), the inside surface of the window is 10°C (283K--not at all unrealistic) and the air temperature, and all other surfaces, in the room are 26°C (299K), just what the thermostat orders. There is a hard-working executive, practicing his putting, at the window. What temperature does this fellow feel?

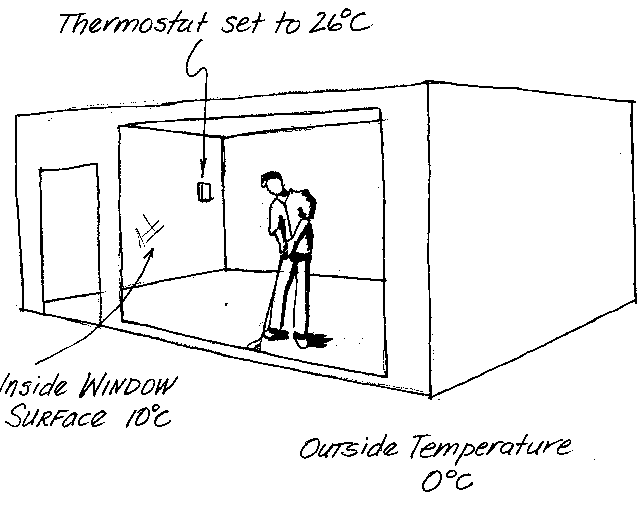
It all depends on what the window is like. If it is completely transparent to infrared radiation (e is nearly zero) then the window and the person will transfer heat between them like the window is 0°C (273K). Since the window is very large, it forms nearly a hemispherical view. Meanwhile, the remainder of the room is a hemispherical view of a blackbody at 26°C (299K). On average the person transfers heat to the room like it is a mere 13°C (286K). The room may even feel colder because people are quite sensitive to small surface areas of skin that are too cold.

If, on the other hand, the window is made of one of those high e glasses like PPG's Sungate®, which are coated with stannous oxide, then it will radiate near its actual temperature (283K). Yet the room may still feel too cold. In this case, what room comfort probably requires is a double paned glass, which allows the inside surface to reach a temperature near the thermostat setting. In fact, in this case we may be able to lower the thermostat because the room will have no cold spots. The important point to remember is that air temperature can be a poor guide to comfort.

What's the heat transfer thing if we are outside?

The natives in many dry climates can make ice at night, even when the air temperature remains near 55°F, by exposing a shallow earthen dish of water on a high piece of ground to a clear, dry, night-time sky. In July 1995, my brother found a dead person lying atop a hill. He, too, had been exposed to a clear, dry, night-time sky; and the sheriff concluded that the person had died of exposure on a night when the air temperature in all likelihood stayed near 50°F all night. What do these have in common?

Figure 4, in the upper part, shows a person outside in sunshine. It is well known that about 40-50% of heat loss from a human occurs through radiation. Therefore, radiation is very important for maintaining our body temperature. During the day there is a 6000K sphere in view that is 0.5°of arc. It is the sun. There is diffuse radiation coming from other parts of the sky as well. Also, the earth, and vegetation are warmed by the sun, and all radiate also. Thus, even if the air is not particularly warm, a person can feel comfortable on a sunny day because some object at every possible view is radiating.

Now let us examine the same situation at night. The person, having a nearly constant surface temperature radiates at the same rate as before. Skin, by the way, is nearly a blackbody at long wavelengths(e=1). But now there is no sun to radiate energy, there is little or no diffuse light from the sky, and the earth and plants are all much cooler. Does any radiation come from the sky?

The answer depends on what is in the sky. Probably the most important thing is how much water vapor is in the air? Water vapor is a very important absorber of infrared radiation, which means also that it is a very important emitter. If the air near the ground surface is very wet, then a thick layer of air will radiate just like a blackbody of the same temperature. This is why the evening cools-off so little in places like the Southeast or Midwest. If, on the other hand, the air is quite dry, as it is in Wyoming or in desert areas, then it absorbs and radiates almost nothing. In this case that 50% radiated energy from the body is a very substantial heat loss, which has to be is replaced from within the body. Is the body up to the task?

The dead person my brother found on the hilltop, had gotten his car stuck in mud during the night. As he struggled to free the car he apparently had beer to drink--quite a lot of beer i think--and he also became very warm. As he continued to wrestle the car he took off clothing. Finally he wandered up a nearby hill, with substantial blood alcohol, nearly naked, and passed out on the hill top.

Put as simply as possible the chain of causation here is...

Wyoming-->Dry, Clear, Night-time sky-->Go naked-->Die.

Keep your clothes on, folks, they make a good radiation baffle!

The katabatic wind: or heating by cooling.

This is not a paradox of radiation per se, but it involves radiation along the same lines as the previous paradox. Consider how air, near the ground surface, behaves on a summer night in Wyoming. The ground surface radiates to the night sky, cools rapidly, and cools the neighboring air. We have just seen that this occurs in a most pronounced way when the air is dry, as it often is in Wyoming. As this air cools it does so near a particular ground elevation. In other words, it cools at constant pressure. We can organize the ideal gas law in this situation to...

rT=constant.

The air becomes more dense as it cools along an isobar. In figure 5 as the air cools it follows the iosbar (a hyperbola) from 1 to 2. The ground probably slopes in some direction, and the air, having now become more dense flows downslope to lower elevation. It is extremely difficult to maintain static air on sloping ground when there is radiation heat transfer, and this is one reason (among millions of others) why Wyoming is windy. This wind is called a katabatic wind.

In order to understand what happens as air sinks downhill, you first must recognize that air pressure increases with lowering elevation. The reason, simply put, is that air pressure has to support the weight of all of the air above, and at lower elevation there is more air mass to support.

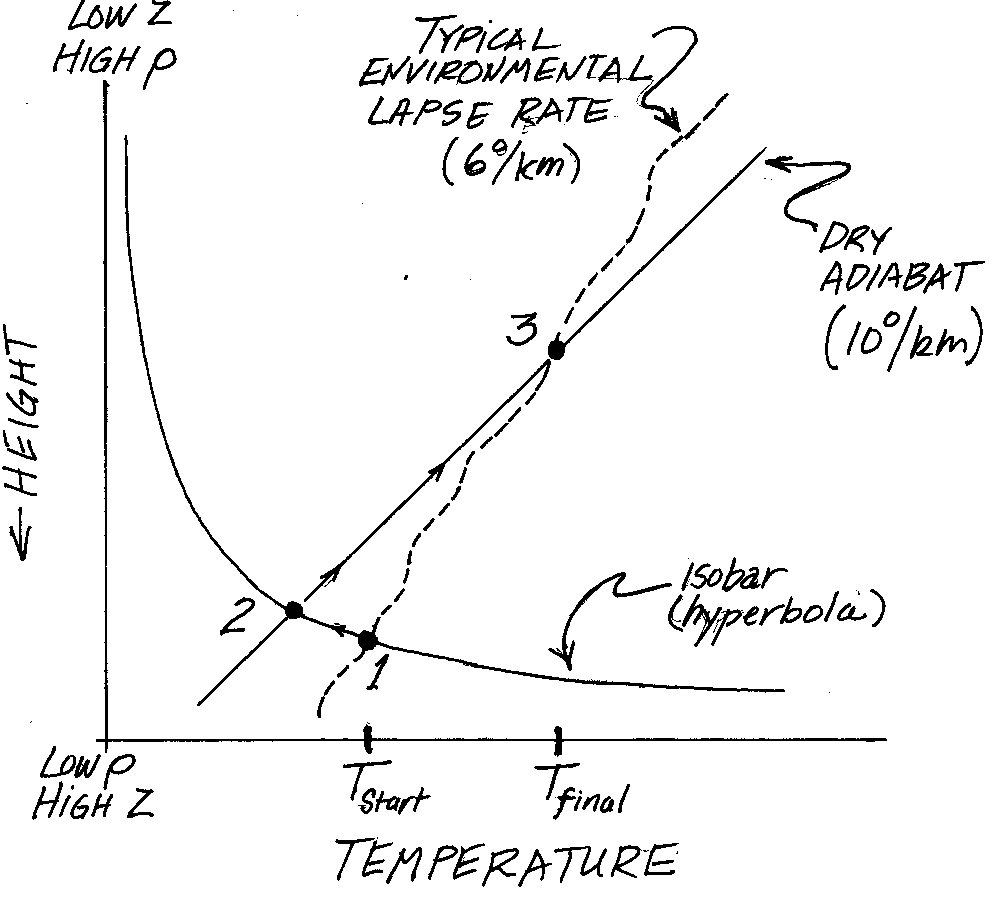
What happens to the parcel of air that became too dense and is now sinking down a sloping surface? Well, its pressure certainly rises, but what else occurs? The answer could become very complicated, but if we assume it sinks so rapidly that it cannot transfer heat, then the first law of thermodynamics tells us what occurs. The first law is dU=dq-dw. I know you didn't fully understand this at the time, but dU is an exact differential which is a difference of two inexact ones. The inexact differentials we can calculate only when we know how heat is transfered or work is done. In this particular case we set dq equal to zero because we are not transfering heat. The inexact differential dw is quite easy to state--if we use heat content (H) rather than internal energy (U), then the only work involved is mgdz; where m is a mass of air (who cares how much?) and g is gravitational acceleration. Ah, you will recognize no doubt, that work in this case is just like lowering a mass in physics lab. Meanwhile, the exact differential we can calculate independently of how the air arrived at its current state. Being an ideal gas (ideally that is) its heat content is just dH=mc_pdT. Now reorganize this to dT/dz=-g/c_p. Meteorologists call this the dry adiabatic lapse rate, and it describes how the temperature of air will change if it is moved quickly to a new elevation. It is the straight line on Figure 5. The sinking parcel of air follows this line from 2 to 3 on the diagram.

So, we conclude that the sinking air will undergo a change of temperature and a change of pressure, which means its density changes. Moreover, it will not stop flowing downhill until its density equals that of the surrounding air. When will this occur, you ask? Figure 5 also shows a sort of ragged line that is meant to indicate how the state of the surrounding air varies with height. Meteorlogists call it the environmental lapse rate, and it has a value near 6C/km.

You might ask, why does the environmental lapse rate not equal the adiabatic rate? This is a good question, because it is easy for me to answer. The reason is that the envirnoment has evolved to its current state though a whole series of unknown processes, or, in other words though a whole bunch of steps of dq and dw, and the environmental lapse rate simply represents the end result of it all.

On Figure 5 I show that the sinking air stops sinking where these two curves cross. Always that happens when the sinking air reaches a greater density and higher temperature than it had when it began radiating early in the evening. The air has warmed by loosing heat! Isn't radiation weird?

Almost any summer night, you can go to the Goshen Hole country in eastern Wyoming, and feel a katabatic wind flowing down the drainages of Horse Creek and Bear Creek. In drought years, when the air is especially dry, this wind is at its most severe, as you'd expect. In these years the wind can reach 70mph and adds additional misery for crops and farmers beyond what the drought does already.

A bunch of objects in equilibrium with radiation don't have the same temperature!

You learned in physics that objects at thermal equilibrium all have the same temperature. Yet if you examine objects bathed in the radiation field of a summer day, objects which are free to exchange energy and which you'd think of as reaching equilibrium, they aren't the same temperature at all. After all, the white plastic deck chair can feel cold to your touch while the red hood of the sports car is hot enough to fry an egg. What trick is radiation playing now?

Earlier I said that the coefficients describing emissivity, absorbtion, and transmission vary with wavelength. This makes it possible that one material is very absorptive at a particular wavelength and not emissive at another; and a different material is not absorptive at the first wavelength, but very emissive at the second. These two materials will not behave the same.

If we are interested in how materials will behave when in sunlight, then the important figure of performance is the ratio of absorption coefficient in visible light, a_s to emissivity at thermal infrared wavelengths, e_b. Examples of two extreme materials in this regard are aluminum painted with white epoxy paint, for which the ratio is 0.3, and brushed stainless steel, for which the ratio is 4.3. If these two materials are placed in full sunlight, and prevented from cooling by any means other than long-wave radiation, they will achieve equilibrium temperatures of 286K and 564K, respectively! A Carnot heat engine operating between these two temperatures would be 50% efficient, far better than any photovoltaic solar panels.

Conclusions

We are out of time, especially so as I planned some time for questions and answers. In summary, it should be obvious that the subject of radiation heat transfer is very interesting. It is also very complex, and becomes even more so when absorbing gases are present, and when solid surfaces transmit radiation and so forth. These few examples, I hope have shown you how to begin solving realistic, and interesting problems.