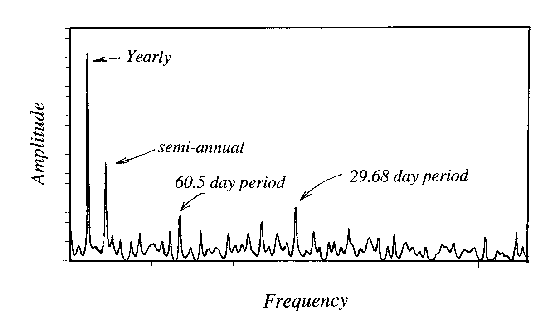
Figure 1. Spectrum of surface pressure as measured at Cheyenne, Wyoming, during a part of the period of 1984-1996.

Figure 1. Spectrum of surface pressure as measured at Cheyenne, Wyoming, during a part of the period of 1984-1996.
The spectral analysis shown in Figure 1 I did on a whim. I had no idea what I would find by looking at the surface air pressure records, but what I saw in this record surprised me greatly. I do not have any answer to this puzzle at all, and my searches of the WWW have turned up suprisingly little to help me. I think this is a first rate amateur science project. I will tell all that I know about the topic in this somewhat long posting.
It is obvious to everyone that the weather varies over a daily cycle and over the course of a year. There are also the weather cycles of frontal systems in the mid-latitudes, which are strongest in spring and autumn and do not follow a regular cycle in time. One might wonder if there are other regular weather cycles too subtle to readily detect.
Figure 1 shows a spectral analysis of surface pressure as recorded at Cheyenne, Wyoming during some part of the period 1984 to 1996. There are several sharp signals in the spectrum. I cannot quote the period of these signals precisely because of the scale of this plot and limited resolution of my method, but the most obvious cycle lies between periods of 356 and 374 days. This is the well known annual cycle of surface pressure which results from the changing temperature of the ground surface and atmosphere through the year. Weather stations above 400m elevation have lower pressure during the winter; stations below 400m show the opposite. The next peak occurs near 182 days, or twice per year. It is the first harmonic of the annual cycle; and results from surface temperature not following the changing insolation exactly. The next largest signal occurs at a period near 29.68 days. The length of the data stream (somewhere near 12 years) permits an ultimate resolution of only 0.02 cycles per day. Thus I can say with some authority that the true period of this signal is between 29.48 days and 29.88 days (remember that period=1/frequency). This brackets one cycle per lunar month and suggests very likely that the cause involves the lunar tide. This explanation may leave us to wonder why there is no prominant peak near 14.84 days as well, which would represent the semilunar month. The only other interesting signal occurs near 60 days. I have no idea what it represents. It may be the sixth harmonic of the annual cycle, but that leaves us to wonder why the other intermediate harmonics are not also present.
As I said earlier, the large pressure variations that accompany mid-latitude storms do not occur on regular cycles and contribute only to the noisy background of this spectrum. An enormous amount of daily weather information, including temperature, precipitation, winds, and pressure are available on-line in records of the national climatic data center at http://www.ncdc.noaa.gov/. These pressure data are from Summary of the Day (SOD) archives, which are data set TD-3210.
Just as our moon and sun cause ocean tides, they also cause tides in the solid earth and in the atmosphere. Since a general discussion of tides will only slow us down at this point, I plan to merely summarize the tidal components that a person often observes in the ocean. For someone who is interested in an elementary explanation of tides more thorough than mine please visit this web site. If you desire a more mathematical description, please refer either to Appendix II at the end of this document, or I refer you to Lamb's book on Hydrodynamics.
There is a semi-diurnal tide (twice per day) which results from a combination of lunar and solar gravity, and the curved path in space the Earth follows as a result. There is also a once per day (diurnal) component which results when the moon and sun are not directly over the equator. Because the moon revolves around the Earth once per lunar month, there is also a semi-monthly and monthly component to the tides. These components are more or less visible over the entire oceans depending on local influences such as shape of shoreline, depth of local ocean and so forth.
We expect to observe all these same tidal components in the atmosphere as well, but there are some differences. First, let me summarize what seems known about the short period tides in the atmosphere. By short period I mean tides that go though a cycle in one day or less. The semi-diurnal lunar tide (L2) is the only lunar component that is observable, and it is only possible to observe easily in the tropics. The other lunar tides are too small to observe in ordinary weather records. The diurnal solar tide (S1) is large enough to observe but has an amplitude that varies quite a lot from one place to another. This seems to imply that it results not from the sun's gravitational field (tide), but from local variations in how the sun heats the earth and air. The semi-diurnal solar tide (S2) is small, but it is much larger than (L2), which is somewhat unexpected. Lord Kelvin suggested in the 19th century that this was because the atmosphere had a resonance near a period of 12 hours that couples only through heating of the atmosphere. These tides amount to only 1mb (1 millibar) of pressure variation in the tropics, where they are largest, and only a hundredth of that or so in mid latitudes.
The solar tides, which actually result from heating, not gravity, are quite interesting. They all appear to be harmonics of a 24 hour solar day. Some of the components propagate westward with the sun each day. Other components are called non-propagating. They too are harmonics of the 24 hour day, but they remain stationary at one locale. Although non-propagating components are particularly mysterious, they appear to result from local release of latent heat that the solar tide triggers.
By analogy with the short period tides, you might expect to observe long period tides in the atmosphere as well. There is an annual tide from the annual variation in solar insolation, which I alluded to in the first paragraph. Figure 2 shows the average of station pressure at Peterson Field in Colorado Springs, Colorado over a 15 year period from 1950 to 1965. It shows this annual variation of solar tide. The peak amplitude occurs in the first week of August when it is about 0.30inHg or 10mb above the least mean amplitude which occurs sometime in mid February. You will also notice that the pressure variation does not follow a perfect sinusoid, but instead, the pressure rise is quite steep in late June, and falls quite abruptly in mid November, just about the time of the first big storm each winter season. This lack of sinsoidicity leads to a second harmonic in the annual cycle, so there is a semi-annual component which is very prominent in Figure 1. I will refer to some results in this data later.
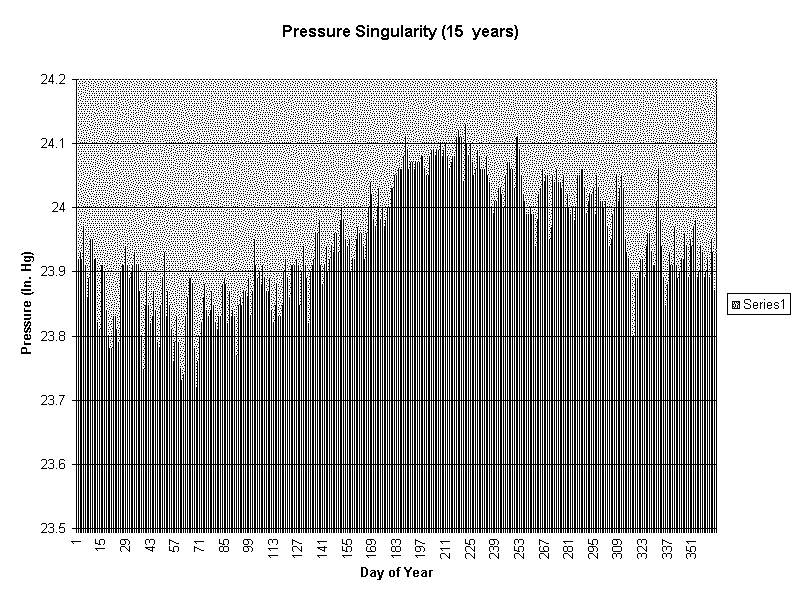
Figure 2. Singularity diagram built by averaging surface pressure each day of the year over 15 years (1950-1965) at Peterson Field, Colorado Springs, Colorado.
According to all sources I have read to this point this annual cycle (and perhaps its first harmonic) is the only long period tide observed in the troposphere. There are monthly tidal components observed in the mesosphere and thermosphere, but these supposedly do not appear at the Earth's surface.
Now I will point to Figure 1 again and ask what this represents. Is this apparent 29.68 day period truly the lunar tidal period? It is perhaps fortuitous that I produced the spectrum of Figure 1 on my first attempt. I have not kept any notes regarding exactly how I processed this data. I do not know, for example, whether I used the station pressure or the sea level pressure. I know for certain that I did not use the entire period from 1984 to 1996, but I am uncertain what subinterval I did use. I do know I used the Burg algorithm to calculate the spectrum.
In Figure 1 the 29.68 day component is the third most significant signal, just behind the annual and semi-annual signals. In order to verify what I had done several years earlier, I re-analyzed this data again recently. Figure 3 shows a spectrum, calculated using the Burg algorithm once again, of the 4017 days that comprise the record of 1984 through 1994. The 29.68 day signal is still apparent, but it is slightly less significant than it was in the original analysis. This tells me that the 19.68 day signal, whatever it may represent, varies in significance from one time interval to another. This is, perhaps, even more interesting than having a signal that is extremely consistent.
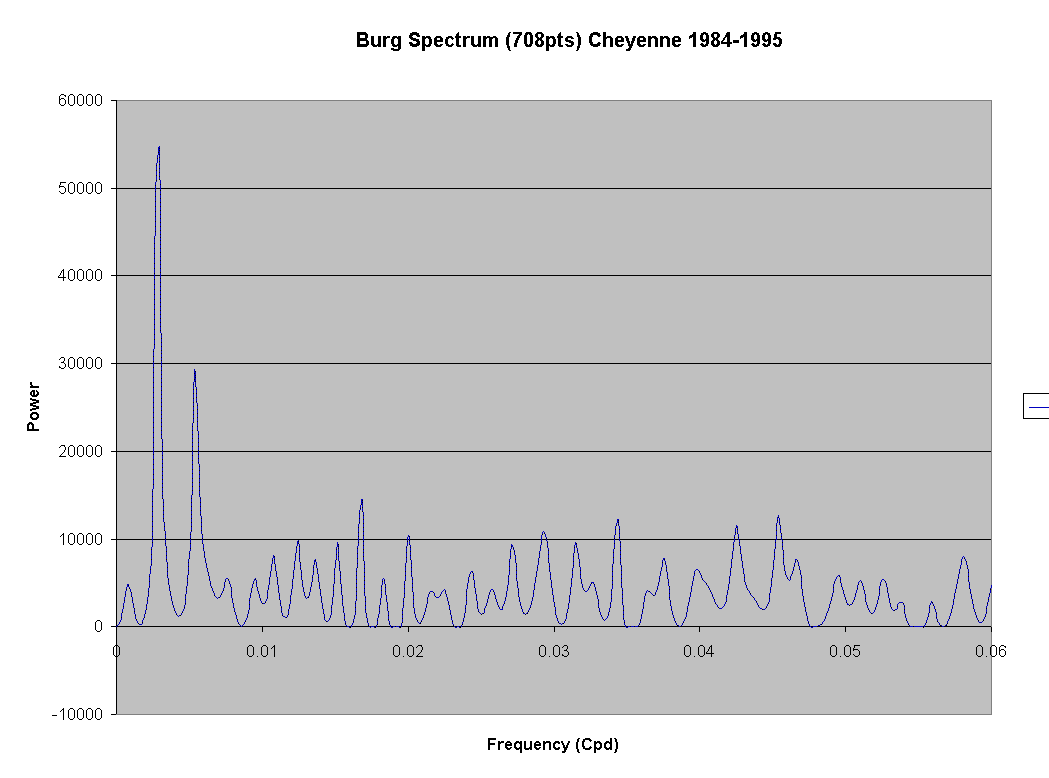
Figure 3. Spectrum of surface pressure as measured at Cheyenne, Wyoming, over the full period of 1984-1994. Burg Algorithm 708 point estimator.
One thing that you may notice about Figure 3 is that there are several apparent signals near 29.68 days. There are also several different ways to measure a lunar month. Most of these measures have a period near 27.5 days. For example, the anomalistic month (one perigee to the next) has a mean period of 27.55 day. Certainly there would be some component of lunar tide that would follow this period, whether or not we could observe it. However, the synodic lunar month, which has a period near 29.53 days is probably the most significant. This lunar period is one that measures the duration between one lunar crossing of the solar meridian to the next. In other words, it is exactly the period of what in the ocean we call the "Spring Tide." While 29.53 days is a mean synodic period, the actual period from one lunar cycle to another can vary by 13 hours. Easily this is enough variation to explain many discrepencies in our observations.
I, personally did not expect to observe a tidal component over the lunar month for the following two reasons. I have had several occasions where I have had to make tidal corrections for geophysical surveys. The largest tidal correction I've ever made was a little over 100microgals, while the Earth's gravitational acceleration is about 1000gals. The tidal effect is only about 10-7 that of the Earth itself. A sobering thought is that the open ocean tides are a mere 0.10m height. I have added a second appendix to this note which outlines a more exact theory, but needless to say, we expect atmospheric tides to be quite small and difficult to observe. My point is that tides are a miniscule effect compared to the 5 to 10mb variations of storm systems. However, the 29.68 day signal is quite apparent on Figures 1, and 3.
You may have already begun to wonder what a spectral analysis of the singularity diagram in Figure 2 shows. This is extremely interesting, because the singularity diagram begins on the same day each year. If any cycle has a phase that varies from one year to the next it is removed through averaging in the preparation of this diagram. So, only signals that are some multiple of a yearly cycle can show up. First there is an annual component. The next most significant component is twice per year, and the next two, which are about equal in significance, are 4 cycles per year and 19 cycles per year. The 6 times per year component, which is visible in both figures 1 and 3, isn't here at all. Either it didn't exist in the period 1950-1965, or it didn't exist at Colorado Springs (Only about 150 miles south of Cheyenne), or it has random changes of phase that average away in the singularity diagram. This 60 day cycle is interesting in its own right.
As I said earlier, I have very little information regarding this phenomenon, and I can find precious little on the world wide web. In fact, a search of the web soon becomes frustrating because I have found that so many people use the term "atmospheric tide" to mean the anomalous ocean tide which results from the pressure disturbance of a moving storm system. These people are not describing a tide in the atmosphere, which is what I am interested in here, but rather one in the ocean. I have found a few references to long period tides in the atmosphere. For example, tides in the mesosphere and thermosphere are mentioned. There is also a book in which Richard Lindzen has written about tides in the atmosphere which may be a good source of information, and an even older book by Sydney Chapman. I hope to get one of these books soon. I do not expect that we are blazing new scientific trails here, but it may be that no one has paid much attention to such long period tides in the atmosphere.
Here is a list of things to ponder. First, the observation may be spurious. Perhaps the suggested spectral component is...
In conclusion, I have observed an unexpected phenomenon,which I have assumed is related to the monthly lunar tide, and which is rarely if ever mentioned in text books or on the WWW. I know very little about the phenomenon and I know there is an enormous field of research that could be conducted using data that is already on the WWW. If anyone is interested in pursuing any of this project let me provide you a little information to get started.
I have mentioned how to find the SOD data at NOAA. When I first looked at the data that comprise Figure 1 several years ago this data was free to download. It generally costs money to download now, and the cost is roughly 0.10 dollars per KiloByte. Yes, you and I know the true cost of delivering data over the internet is just about zero, but NOAA has the data and they call the shots here.
There is a way around this. You can download huge monthly files of global SOD data from NCDC from a data set different than TD-3210. There are restrictions that this data not be shared with commercial entities. The monthly files are available from 1994 to the present time. Each file is about 5+ MBytes in WinZip format and contains SOD data from 1000 or more stations from around the world. It is a huge data resource, and a cooperative effort among several people interested in weather could download it all and share it.
Whether you decide to purchase SOD records from NCDC, or download the free global SOD records, you should begin with a download of a file of station names which is available for each, and download a file containing a description of the data and its format. This will help you find exactly the station name of a locality you wish to analyze and what data are actually available. Please keep in mind that the SOD archival data is not comprehensive. There are many stations that have kept only daily temperature data for most of their existence. Other stations have an extremely complete set of data. You will have to search a data file to see if it contains appropriate data.
I can supply a program which can read TD-3210 SOD data records and build an ASCII file of raw data. I will soon write a similar program to handle the global SOD records if they are different in any way. I will supply source code as well as a 16-bit executable which you can run from a DOS prompt under DOS, Windows, or NT. You may find the FFT and Burg algorithms, along with instructions at my web site. If, after reviewing all of this information, you yet have questions, please send me an e-mail message, and together we can walk though things to get you started.
Very truly yours,
Kevin T. Kilty
A spectrum is a collection of simple components that are added together to produce a complex signal. When we use the term spectrum we typically mean sine and cosine functions as components, but there are other possibilities. One new, and interesting example are the components called "wavelets."
The prototype spectrum is the collection of various pure colors of light that go into making white light, and which a prism or grating will separate. In all of the cases that I discussed in this note the signal is a time series. They are numerical values of some quantity collected at equally spaced time intervals.
Strictly speaking, a true spectrum exists only for time series that are statistically the same over all time intervals, and which have existed for all time. Since neither of these restrictions obtain in practice, we can do no better than estimate the true spectrum. How well we estimate depends on three things:
Aliasing is a difficult concept to grasp, but it is essential to understanding spectral analysis. All of the data that we work with consists of numbers taken at discrete instants of time. Generally the time interval is a constant. However, the phenomenon that we are observing has a value at all intermediate times. It is obvious that if we collect data too infrequently, we cannot detect rapid variations in between the successive samples. But, the situation is actually worse than this. If we sample too slowly we risk confusing very fast variations with very slow ones. A simple example is easy to come by. Suppose that the signal we sample is a sine function with a period of 1 second. Suppose that we sample this each second and estimate the spectrum. We think that the spectrum would show a single component with a period of one second. But we are sampling so slowly that each number is the same, and instead of detecting a variation, we estimate that the data are constant in time. A one second period sign wave is aliased to look exactly like a DC signal in this example.
This confusion in assigning frequency is called "aliasing." To avoid it we have to sample frequently enough that no significant components are missed; or we have to electronically filter the data prior to taking samples. The highest possible frequency we can assign without ambiguity is one cycle for each two samples, and is called the Nyquist frequency.
The effect of aliasing is generally not easy to describe, but almost everyone is familiar with two examples. Phantom patterns in an image can result from aliasing. Moire patterns, for example, result from aliasing a periodic spatial image. Another example is a strobe light which samples a rotating object so slowly that it aliases the motion and makes it appear stationary. Thus, sometimes aliasing is useful.
We collect data for only a brief span of time. If our data are varying extremely slowly, we cannot expect to detect this variation accurately in a brief span of data. Therefore, the span of our data certainly sets a limit to the slowest signal we can detect. Once again, the situation is actually a little worse. The span of data that we measure determines the best resolution we can attain between any adjacent components of a spectrum.
Amateur astronomers will recognize an analogy with telescopes. Having a limited aperture on a telescope limits resolution of closely spaced objects. In an analogous manner signal time span limits the resolution of closely spaced components of the spectrum.
The analogy with optics goes further. In order to improve the resolution of a small aperture, a lense can be darkened progressively from its center to its edge. The resulting apodized objective will provide better resolution of closely spaced objects at the expense of a darker image. In time series, likewise, we may taper data using a window such as the Tukey window (cosine taper), and the Parzen window (cubic polynomial taper). Applying these windows improves resolution, but it does so at the expense of discounting information, especially at the extremes of our data.
There are many ways of estimating spectra, but a common way is to use a Fast Fourier Transform (FFT). An FFT requires evenly spaced data. Sometimes data are evenly spaced when they are collected. However, if they are not, we have to interpolate the data. This links a spectral estimate with the performance of an interpolating algorithm.
An FFT has a further effect. If we have samples of data over a particular time span, the FFT algorithm implicitly assumes that the data are periodic and have a period equal to this same time span. For example, if I extract a segment of tide data that is three months in length, the fourier transform assumes that the tides just repeat in this same pattern every three months. Obviously this is not so, and it leads to some error in estimating the true spectrum. One might conclude that an FFT is like a Fourier series that has been truncated at the Nyquist frequency. However, this characteristic of the FFT to make all signals periodic makes it behave as a trigonometric interpolator. It produces a spectrum that is an aliased Fourier series.
An FFT also errs in estimating the spectrum in another way. If the beginning and end of the sampled signal are not equal, the time series is discontinuous, and the FFT will calculate too much power in the high frequency part of the signal. The same thing happens if any derivatives of the data are discontinous.
Another way to estimate a spectrum is as follows. We imagine that we can pass our series of data through a device designed to figure out what information there is in the data and remove it. What comes out of the box, then, is a series of random numbers completely devoid of information. Such a device is the inverse of my acoustic box! We put in a signal and what comes out is white noise.
The only device that could do this is one that acts like the inverse of the spectrum. So if we know the operation of the device we also know the spectrum.
There is a computer algorithm, due to John Burg, which can figure out how to remove all the information from a signal. Once the algorithm figure how to do this, we can use its design to obtain the spectrum of the data. One advantage of this method is its ability to precisely locate peaks in the spectrum. The spectra of pressure cycles results from the Burg algorithm.
In this appendix I will do what I said in the opening paragraph would only slow me down. I will discuss some mathematical aspects of atmospheric tides. To find what is known as the tide-raising potential, I shall use the classical theory of gravity, confine it to the Earth-Moon system, and ignore rotation of the Earth. First let me write the potential due to the Earth at a point (P) on its surface.
F=GM/r; r=radius of the Earth, M=its mass, and G=universal gravitational constant.
From this potential we can obtain Earth's gravitational field (acceleration) as g= - dF/dr = - GM/r2. We can write a very similar equation for the potential due to the Moon at the same point
W = Gm/R; m=Moons mass and R=distance from the Moon to P.
It is extremely inconvenient to carry around two equations written in terms of two distances, so we will do something that is common in physics, we will use a Taylor expansion to write R in terms of D (earth-moon distance), r, and a. The relationship is suggested in Figure 4.
W = - Gm(r/D)3(cos2a-1/3)/r
Air is a fluid and it will organize itself at equilibrium so that an equipotential surface is also a surface of constant pressure. In my idealized model, composed of a spherical earth that does not rotate, if the Moon were not present the equipotential surfaces would be spherical shells, the height of which we would find as z = F/g. However, the presence of the Moon disturbs this situation so that the true potential heights are z = (F+W)/g. The disturbed geopotential height is W/g, and you may calculate its amplitude range between a = 0, directly beneath the Moon, and a = p/2. The result is 0.7m. This 0.7m of air at sea level produces a pressure of 0.08mb. Thus, the equilibrium tide model produces a lunar (L2) amplitude of 0.08mb pressure--a very small pressure indeed.
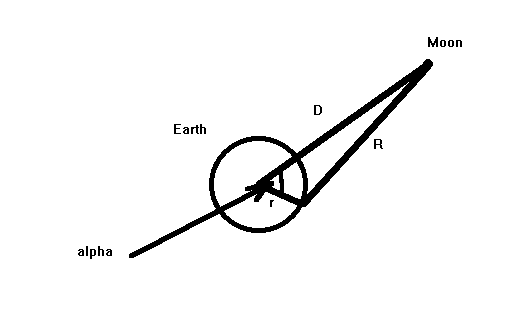
Figure 4. Earth-Moon system and explanation of mathematical notation and symbols.
The simple equilibrium tide I have outlined above hardly applies to the real Earth for two reasons which follow. I will not go into any details here.
I'll stop at this point. I think you amateur scientists should be convinced at this point how complex the study of atmospheric tides could become.